En la Prueba Escrita del Concurso Docente te serán evaluados todos los conocimientos relacionados con la competencia de Razonamiento Cuantitativo. Estas preguntas estarán relacionadas con la capacidad de usar los conocimientos de matemáticas para resolver problemas de la vida cotidiana.
Pregunta 1.
Cuatro amigos van al cine y les han dado cuatro sillas consecutivas. Si la suma de los números de las sillas consecutivas es 126, al segundo amigo le tocó la silla número
Respuesta correcta: B
Justificación:
Como son 4 números consecutivos, llamemos x al menor de los números y que esté sea el primero, entonces el segundo número será x+1, el tercer número será x+2 y el cuarto número será x+3. Ahora bien, como la sumatoria del número de las sillas es 126, entonces planteamos la siguiente ecuación:
(x)+(x+1)+(x+2)+(x+3)=126
x+x+1+x+2+x+3=126, sumamos las variables x y sumamos los términos independientes
4x+6=126, trasladamos el 6 que está sumando a restar al otro lado, junto a 126 como sigue:
4x=126-6, restamos 126-6 que nos da 120
4x=120, trasladamos el 4 que multiplica a la x, a dividir a 120
x=120/4, realizamos el cociente
x=30, como x representa el número menor entonces el segundo número es 31, el tercer número es 32 y el cuarto número es 33. En conclusión el segundo amigo le corresponde la silla 31. Por esto, las demás opciones son incorrectas.
Pregunta 2.
En una reunión familiar hay tres hombres y tres mujeres. Por protocolo se van a asentar alternadamente un hombre y una mujer en una mesa redonda. El anfitrión de la reunión calcula que el número de formas en que pueden sentarse las 6 personas en la mesa redonda alternando los sexos es de
Respuesta correcta: D
Justificación:
Como es una mesa redonda y se alternan los sexos, lo primero es colocar una persona como punto de referencia para ubicar las demás personas. Esta persona como punto de referencia puede ser hombre o mujer, en este caso fijamos inicialmente una mujer y podemos calcular las posiciones de los demás invitados. Como el orden importa en como van ubicados en la mesa y no hay repetición, hacemos una permutación, tanto para los hombres como para las mujeres. Ahora bien, si fijamos inicialmente a una mujer tenemos que hacer una permutación con las dos mujeres que quedan y una permutación con los tres hombres y luego estos resultados los multiplicamos.
En primer lugar hacemos la permutación de las dos mujeres que sería una permutación de 2 con 2, porque son en total dos mujeres que se van a sentar del grupo de 2 mujeres porque ya una mujer quedó fija, como sigue:
nPr = n! / (n-r)!
como n=2 y r=2, reemplazamos en la fórmula
2P2 = 2! / (2-2)!, realizamos la diferencia en el denominador
2P2 = 2! / 0!, recordemos que 0! es 1 y que 2! es 2*1
2P2 = (2*1) / 1, multiplicaos 2*1 y dividimos entre 1
2P2 = 2 En conclusión existen 2 maneras de ubicar 2 mujeres de un grupo de 2 mujeres en la mesa redonda.
En segundo lugar, hacemos la permutación de los tres hombres restantes, el cual hacemos una permutación de 3 con 3, porque son tres hombres de un grupo de tres hombres, quedando así:
nPr = n! / (n-r)!
como n=3 y r=3, reemplazamos en la fórmula
3P3 = 3! / (3-3)!, realizamos la diferencia en el denominador
3P3 = 3! / 0!, recordemos que 0! es 1 y que 3! es 3* 2*1
3P3 = (3*2*1) / 1, multiplicamos 3* 2*1 y dividimos entre 1
3P3 = 6 En conclusión existen 6 maneras de ubicar 3 hombres de un grupo de 3 hombres en la mesa redonda.
por último multiplicamos el número de permutaciones de las mujeres con el número de permutaciones de los hombres
2P2 * 3P3 = 2 * 6 = 12, en conclusión existen 12 maneras distintas de sentar a tres hombres y tres mujeres en una mesa redonda, alternando los sexos. Con base en el proceso anterior, las opciones restantes son incorrectas.
Pregunta 3.
Un ingeniero estudia el cono para crear una pieza mecánica. La información que recopila el ingeniero se resume en la siguiente imagen
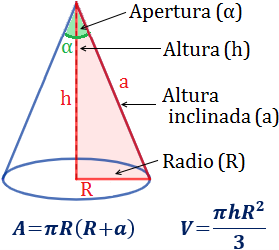
tomado de: https://www.problemasyecuaciones.com/geometria3D/volumen/cono/area-problemas-resueltos-calculadora-formulas.html
Donde A es el área superficial y V el volumen.Si la pieza que diseña el ingeniero tiene una altura inclinada (a) de 13 cm y una altura (h) de 5 cm entonces el cono tiene un área superficial de
Respuesta correcta: D
Justificación:
Como vemos en el cono las medidas de la altura (h) el radio ® y la altura inclinada (a) forman un triángulo rectángulo, donde la altura inclinada es la hipotenusa, la altura y el radio son catetos. Entonces usando el teorema de pitágoras, hallamos el radio como sigue:
altura inclinada2 = altura2 + radio2
como la altura inclinada es 13 cm y la altura es 5 cm entonces el radio se puede calcular así:
(13 cm)2 = (5 cm)2 + (radio)2
169 cm2 = 25 cm2 + radio2
169 cm2 = 25 cm2 = radio2
144 cm2 = radio2
aplicamos raíz cuadrada a ambos miembros de la igualdad para conocer el valor de la altura de la pared
√144 cm2 = √radio2 nos queda
12 cm = radio
como el radio es 12 cm y el área se puede calcular con la fórmula
A = πR(R + α), como R=12 cm y a=13 cm reemplazando nos queda
A = π(12 cm)(12 cm + 13 cm)
A = π(12 cm)(25 cm)
A = (300 cm2)
A = 300π cm2
Pregunta 4.
Un ingeniero diseña una caja de base cuadrada para empacar leche como se muestra a continuación
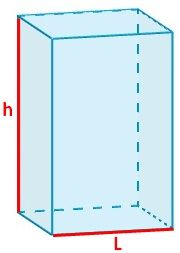
Fuente: https://www.universoformulas.com/matematicas/geometria/area-prisma-cuadrangular/
Teniendo en cuenta que la medida de L es 12 cm y la capacidad de la caja debe ser 1,5 litros, entonces la cantidad de metros cuadrados de cartón que necesita para la fabricación de la caja esRespuesta correcta: B
Justificación:
Como el volumen de la caja debe ser 1,5 litros, y un litro equivale a 1.000 cm3 entonces haciendo la conversión a centímetros cúbicos nos queda:
1,5 * 1000 = 1.500 cm3
De manera que el volumen de caja es 1.500 cm3
Ahora el volumen de la caja se obtiene así:
Volumencaja = área de la base * altura, como la base es cuadrada de lado 12 cm y el volumen es 1.500 cm3, entonces hallamos la altura de la caja:
Altura = Volumencaja / área de la base
Altura = 1.500 cm3 / 12 cm * 12 cm
Altura = 1.500 cm3 / 144 cm2
Altura = 10,42 cm
Ahora, para hallar la cantidad de material para hacer la caja, hallamos el área total de la caja como sigue:
Áreatotal = Árealateral + 2Áreabase
Áreatotal = perímetrobase * h + 2Áreabase, como el perimetro de base es 48 cm, la altura 10,42 cm y el área de base 144 cm2, entonces reemplazamos los valores
Áreatotal = 48 cm * 10,42 cm + 2(144cm2)
Áreatotal = 500,16 cm2 + 288 cm2
Áreatotal = 788,16 cm2
Ahora para convertir 788,16 cm2 a m2, dividimos 788,16 entre 10.000
788,16/10000=0.078816
o sea que 788,16 cm2 equivale a 0,078816 m2, que es la cantidad de cartón que se necesita para hacer la caja.
Pregunta 5.
Se lanzan dos monedas y un dado de seis caras numeradas del 1 al 6 al mismo tiempo. La probabilidad de que salgan las dos monedas con la misma cara y un número par en el dado es del
Respuesta correcta: C
Justificación:
Una moneda al ser lanzada sólo tiene dos posibilidades -cara o sello- y el dado tiene 6 posibilidades de salir. Entonces para calcular las posibles combinaciones entre el lanzamiento de la moneda y el dado aplicamos el principio de multiplicación. El principio de multiplicación es una técnica de conteo que se usa cuando un suceso “x” se puede hacer de m formas diferentes y otros suceso “y” se puede hacer de n formas distintas entonces el número total de formas es mxn. Entonces aplicando el principio de multiplicación nos queda que:
| Moneda 1 | Moneda 2 | Dado | Posibilidades |
|---|---|---|---|
| cara | cara | 1 | 2*2*6=24 |
| sello | sello | 2 | |
| 3 | |||
| 4 | |||
| 5 | |||
| 6 | |||
| 2 posibilidades | 2 posibilidades | 6 posibilidades |
Hay 24 posibles combinaciones al lanzar 2 monedas y un dado de seis caras.
Ahora para que salga la moneda con la misma cara, hay dos posibilidades, que salga cara-cara o sello-sello y la posibilidad de que salga un número par en un dado es 3 que son 2, 4 y 6. Entonces multiplicamos ambas posibilidades 2 y 3 que nos da 2*3= 6, o sea que del lanzamiento de dos monedas y un dado, la posibilidad de que salga la misma cara en la moneda y un número par en el dado, es 6 de 24.
Ahora bien, como la probabilidad se define como el cociente entre los casos favorables sobre los casos posibles y al lanzar dos monedas y un dado tendríamos 24 casos posibles, pero el hecho de que salga dos monedas con la misma cara y un número par tendríamos 6 casos favorables, entonces aplicando la definición de probabilidad, nos queda que:
Probabilidad = casos favorables / casos posibles
Probabilidad = 6 / 24 = 0,25 * 100 = 25%
O sea que hay un 25% de posibilidad que salga la misma cara en la moneda y un número par en el dado.